Although it is not too difficult to determine a wheel or an axle load for an individual vehicle, it becomes quite complicated to determine the number and types of wheel/axle loads that a particular pavement will be subject to over its design life. Furthermore, it is not the wheel load but rather the damage to the pavement caused by the wheel load that is of primary concern. The most common historical approach is to convert damage from wheel loads of various magnitudes and repetitions (“mixed traffic”) to damage from an equivalent number of “standard” or “equivalent” loads. The most commonly used equivalent load in the U.S. is the 18,000 lb (80 kN) equivalent single axle load (normally designated ESAL). At the time of its development (early 1960s at the AASHO Road Test) it was much easier to use a single number to represent all traffic loading in the somewhat complicated empirical equations used for predicting pavement life.
There are two standard U.S. ESAL equations (one each for flexible and rigid pavements) that are derived from AASHO Road Test results. Both these equations involve the same basic format, however the exponents are slightly different.
Load Equivalency Factors
The equation outputs are load equivalency factors (LEFs) or ESAL factors. This factor relates various axle load combinations to the standard 80 kN (18,000 lbs) single axle load. It should be noted that ESALs as calculated by the ESAL equations are dependent upon the pavement type (flexible or rigid) and the pavement structure (structural number for flexible and slab depth for rigid). As a rule-of-thumb, the 1993 AASHTO Design Guide, Part III, Chapter 5, Paragraph 5.2.3 recommends the use of a multiplier of 1.5 to convert flexible ESALs to rigid ESALs (or a multiplier of 0.67 to convert rigid ESALs to flexible ESALs). Using load spectra (as proposed in the 2002 Guide for the Design of New and Rehabilitated Pavement Structures) will eliminate the need for flexible-rigid ESAL conversions. Table 1 shows some typical LEFs for various axle-load combinations.
Table 1. Some Typical Load Equivalency Factors
| Axle Type (lbs) | Axle Load | Load Equivalency Factor (from AASHTO, 1993) | ||
| (kN) | (lbs) | Flexible | Rigid | |
| Single axle | 8.9 44.5 62.3 80.0 89.0 133.4 |
2,000 10,000 14,000 18,000 20,000 30,000 |
0.0003 0.118 0.399 1.000 1.4 7.9 |
0.0002 0.082 0.341 1.000 1.57 8.28 |
| Tandem axle | 8.9 44.5 62.3 80.0 89.0 133.4 151.2 177.9 222.4 |
2,000 10,000 14,000 18,000 20,000 30,000 34,000 40,000 50,000 |
0.0001 0.011 0.042 0.109 0.162 0.703 1.11 2.06 5.03 |
0.0001 0.013 0.048 0.133 0.206 1.14 1.92 3.74 9.07 |
Assumptions
- Terminal serviceability index (pt) = 2.5
- Pavement structural number (SN) = 3.0 for flexible pavements
- Slab depth (D) = 9.0 inches for rigid pavements
Generalized Fourth Power Law
The AASHTO load equivalency equation is quite cumbersome and certainly not easy to remember. Therefore, as a rule-of-thumb, the damage caused by a particular load is roughly related to the load by a power of four (for reasonably strong pavement surfaces). For example, given a flexible pavement with SN = 3.0 and pt = 2.5:
- A 18,000 lb (80 kN) single axle, LEF =1.0
- A 30,000 lb (133 kN) single axle, LEF = 7.9
- Comparing the two, the ratio is: 7.9/1.0 = 7.9
- Using the fourth power rule-of-thumb:
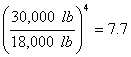
Thus, the two estimates are approximately equal.
LEF Example
Assume a logging truck has three axles:
- Truck tractor
- Steering axle (single axle) = 14,000 lb (62.2 kN)
- Drive axle (tandem axle) = 34,000 lb (151.1 kN)
- Trailer
- Pole trailer axle (tandem axle) = 30,000 lb (133.3 kN)
The total equivalent damage by this truck is (pt = 3.0, SN = 3):
| Steering axle @ 14,000 lb | equals | 0.47 ESAL |
| Drive axle @ 34,000 lb | equals | 1.15 ESAL |
| Pole axle @ 30,000 lb | equals | 0.79 ESAL |
| Total | equals | 2.41 ESAL |
If a pavement is subjected to 100 of these trucks each day (in one direction) for 20 years (5 days per week), the total ESAL for this truck would be:
(5 day/7 day)(365 days/year)(20 years)(100 trucks/day)(2.41 ESAL/truck) = 1,256,643 ESAL
General Observations Based On Load Equivalency Factors
- The relationship between axle weight and inflicted pavement damage is not linear but exponential. For instance, a 44.4 kN (10,000 lbs) single axle needs to be applied to a pavement structure more than 12 timesto inflict the same damage caused by one repetition of an 80 kN (18,000 lbs) single axle. Similarly, a 97.8 kN (22,000 lbs) single axle needs to be repeated less than half the number of times of an 80 kN (18,000 lbs) single axle to have an equivalent effect.
- An 80 kN (18,000 lbs) single axle does over 3,000 times more damage to a pavement than an 8.9 kN (2,000 lbs) single axle (1.000/0.0003 ˜ 3,333).
- A 133.3 kN (30,000 lbs) single axle does about 67 times more damage than a 44.4 kN (10,000 lbs) single axle (7.9/0.118 ˜ 67).
- A 133.3 kN (30,000 lb) single axle does about 11 times more damage than a 133.3 kN (30,000 lb) tandem axle (7.9/0.703 ˜ 11).
- Heavy trucks and buses are responsible for a majority of pavement damage. Considering that a typical automobile weighs between 2,000 and 7,000 lbs (curb weight), even a fully loaded large passenger van will only generate about 0.003 ESALs while a fully loaded tractor-semi trailer can generate up to about 3 ESALs (depending upon pavement type, structure and terminal serviceability).
- Determining the LEF for each axle load combination on a particular roadway is possible through the use of weigh-in-motion equipment. However, typically this type of detailed information is not available for design. Therefore, many agencies average their LEFs over the whole state or over different regions within the state. They then use a standard “truck factor” for design which is simply the average number of ESALs per truck. Thus, an ESAL determination would involved counting the number of trucks and multiplying by the truck factor.
- This method allows for ESAL estimations without detailed traffic measurements, which is often appropriate for low volume roads and frequently must be used for lack of a better alternative for high volume roads.
- When using this method, there is no guarantee that the assumed truck factor is an accurate representation of the trucks encountered on the particular roadway in question.
Estimating ESALs
A basic element in pavement design is estimating the ESALs a specific pavement will encounter over its design life. This helps determine the pavement structural design (as well as the HMA mix design in the case of Superpave). This is done by forecasting the traffic the pavement will be subjected to over its design life then converting the traffic to a specific number of ESALs based on its makeup. A typical ESAL estimate consists of:
- Traffic count. A traffic count is used as a starting point for ESAL estimation. Most urban areas have some amount of historical traffic count records. If not, simple traffic tube counts are relatively inexpensive and quick. In some cases, designers may have to use extremely approximate estimates if no count data can be obtained.
- A count or estimate of the number of heavy vehicles. This usually requires some sort of vehicle classification within the traffic count. The simplest classifications divide vehicles into two categories: (1) heavy trucks and (2) others. Other, more elaborate schemes can also be used such as the FHWA’s vehicle classification.
- An estimated traffic (and heavy vehicle) growth rate over the design life of the pavement. A growth rate estimate is required to convert a single year traffic count into the total traffic experienced over the pavement design life. Typically, multiplying the original traffic count by the pavement design life (in years) will grossly underestimate total ESALs. For example, Interstate 5 at mile post 176.35 (near Shoreline, Washington) has experienced a growth from about 200,000 ESALs per year in 1965 (original construction) to about 1,000,000 ESALs per year in 1994. Thus, over a 30 year period, the ESALs per year have increased by a factor of five or an annual growth rate of about six percent.
- Select appropriate LEFs to convert truck traffic to ESALs. Different regions may experience different types of loads. For instance, a particular area may experience a high number of trucks but they may be mostly empty thus lowering their LEF. For instance, the statewide LEF for Washington State is about 1.028 ESALs/truck. However, this may be drastically different from local LEFs.
- An ESAL estimate. An ESAL estimate can be made based on the preceding steps. Depending upon circumstances these estimates may vary widely. Figure 1 shows an example of a pavement that was built for an estimated ESAL loading but is experiencing a much higher loading due to a marked increase in bus traffic.
|
|


