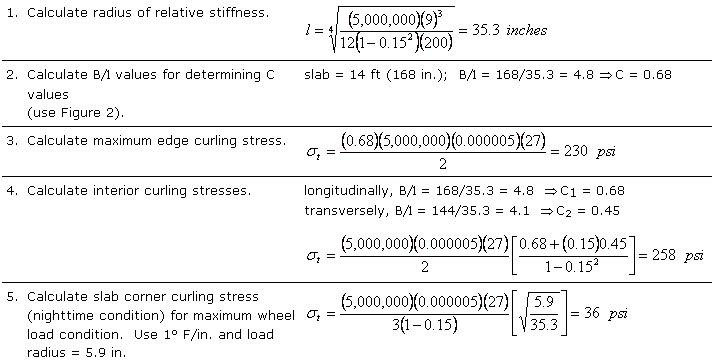The following examples illustrate how rigid pavement responses to different stresses are calculated.
Load Stress Example Calculations
Example 1
Calculate the three critical stresses for 9 inch thick slabs. Use a 9,000 lb. FWD loading (a = 5.9 inches). Use k = 200 pci for calculation of the radius of relative stiffness (l).
| 1. | Calculate radius of resisting sections. | 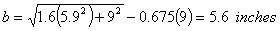 |
| 2. | Calculate radius of relative stiffness | 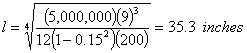 |
| 3. | Calculate interior stress. | 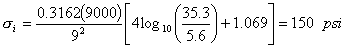 |
| 4. | Calculate edge stress. | 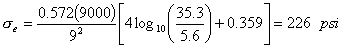 |
| 5. | Calculate corner stress. | 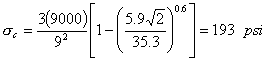 |
This illustrates why the middle of the slab at the longitudinal outer edge (next to shoulder) is considered critical. Further, it illustrates why tied PCC shoulders can reduce critical edge and corner stresses.
Example 2
How would the stresses in Example 1 be reduced if the slab was 12 inches. thick?
| 1. | Calculate radius of resisting sections. | 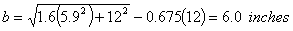 |
| 2. | Calculate radius of relative stiffness | 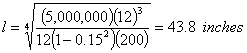 |
| 3. | Calculate interior stress. | 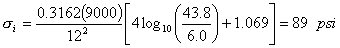 |
| 4. | Calculate edge stress. | 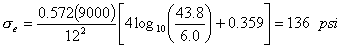 |
| 5. | Calculate corner stress. | 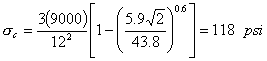 |
Example 3
Using the three critical slab locations, what is the total stress (load plus warping) for the 9 inch slab. The curling stresses are obtained from the Curling Stress Calculation Example.
| Interior (daytime temperature gradient) | ||||
| Load | = | 150 | psi | |
| Curling | = | 258 | psi | (14 ft. long slab) |
| Total | = | 408 | psi | |
| Edge (daytime temperature gradient) | ||||
| Load | = | 226 | psi | |
| Curling | = | 230 | psi | (14 ft. long slab) |
| Total | = | 456 | psi | |
| Corner (nighttime temperature gradient) | ||||
| Load | = | 193 | psi | |
| Curling | = | 36 | psi | (14 ft. long slab) |
| Total | = | 229 | psi | |
Shrinkage and Expansion Example Calculation
Calculate the total joint movement for existing PCC slabs 9, 10, 13, 14 ft. long. Use ΔT = 67°F and ΔT = 45°F, a granular base course and e ~ 5.0 x 10-6/°F.
| ΔT = 67°F | ΔT = 45°F |
| 9 ft. slab | |
| (0.80)(9)(12)(0.000005)(67) = 0.029 in. | (0.80)(9)(12)(0.000005)(45) = 0.019 in. |
| 10 ft. slab | |
| (0.80)(10)(12)(0.000335) = 0.032 in. | (0.80)(10)(12)(0.000225) = 0.022 in. |
| 13 ft. slab | |
| (0.80)(13)(12)(0.000335) = 0.042 in. | (0.80)(13)(12)(0.000225) = 0.028 in. |
| 14 ft. slab | |
| (0.80)(14)(12)(0.000335) = 0.045 in. | (0.80)(14)(12)(0.000225) = 0.030 in. |
Curling Stress Example Calculation
Calculate various warping stresses for a rigid pavement slab with the following parameters and conditions:
- k = 200 pci
- DT = 3° F/in.
- e = 0.000005/°F
- m = 0.15
- E = 5,000,000 psi
- slab length = 14 ft.
- slab width = 12 ft.
- slab thickness h = 9 in.