The AASHTO Definition of reliability is:
“The reliability of the pavement design-performance process is the probability that a pavement section designed using the process will perform satisfactorily over the traffic and environmental conditions for the design period.” (AASHTO, 1993[1])
(Note: design period is defined as the time from initial construction or rehabilitation to its terminal serviceability index.)
Reliability
AASHTO uses the reliability concept to account for design uncertainties. Basically, a pavement structure is designed using the most accurate input data available; data are not manipulated or inflated (nor are conservative values used) to compensate for their estimated variability but rather the best value is used. All variability the pavement structural design process is then accounted for in the “reliability” factor. The reliability factor is comprised of two variables:
- ZR = standard normal deviate. The standard normal table value corresponding to a desired probability of exceedance level. For example, a designer may specify that there should only be a 5 % chance that the design does not last a specified number of years (e.g., 20 years). This is the same as stating that there should be a 95 % chance that the design does last the specified number of years (e.g., 20 years). Then, the reliability is 95 % (100 % – 5 %) and the corresponding ZR value is -1.645 (see 1993 AASHTO Guide, Table 4.1, p. I-62). ‘
- So = combined standard error of the traffic prediction and performance prediction. This variable defines how widely the two basic design inputs, traffic and performance, can vary. For instance, traffic may be estimated at 2,000,000 ESALs over 20 years. However, actual traffic may turn out to be 2,500,000 ESALs over 20 years due to unanticipated population growth. Similarly, pavement design factors may turn out to be different than estimated. What these two brief examples are expressing is that structural design input values can vary from those initially chosen and the equation must account for this somehow. The more these values vary, the higher the value of So.
For example, the basic 1993 AASHTO Guide flexible design equation is: 
The right side of the above equation is then augmented with So (to account for input value variability) and ZR (to establish a confidence level that a certain design will perform as intended) to obtain the final form of the equation:
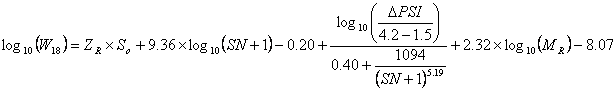
Values of ZR are always negative. Therefore, the quantity (ZR´ So) is always negative and will serve to decrease the predicted number of 80 kN (18,000 lb.) ESALs that a particular design can accommodate. At first glance it may seem unusual that the quantity (ZR´ So) is added to the right side of the equation rather than multiplied. However, if the logarithm on the left side of the equation is removed through algebraic manipulation, it can be seen that the quantity (ZR´ So) would then be multiplied with the resulting equation.
Recommended Values of ZR and So
Each agency that uses the 1993 AASHTO Guide design equation can choose their own levels of reliability to use, however the 1993 AASHTO Guide (Table 2.2, p. II-9) provides some recommended levels (reproduced in Table 1).
Table 1. Suggested Levels of Reliability for Various Functional Classifications (from AASHTO, 1993[1])
| Functional Classification | Recommended Level of Reliability | |
| Urban | Rural | |
| Interstate and Other Freeways | 85 – 99.9 | 80 – 99.9 |
| Principal Arterials | 80 – 99 | 75 – 95 |
| Collectors | 80 – 95 | 75 – 95 |
| Local | 50 – 80 | 50 – 80 |
Typical values of So used are 0.40 to 0.50 for flexible pavements and 0.35 to 0.40 for rigid pavements.
- AASHTO Guide for Design of Pavement Structures. American Association of State Highway and Transportation Officials. Washington, D.C.↵
