Mechanistic models are used to mathematically model pavement physics. There are different types of models available today (e.g., dynamic, viscoelastic models) but this section will present two, the layered elastic model and the finite elements model (FEM), as examples of the types of models typically used. Both of these models can easily be run on personal computers and only require data that can be realistically obtained.
Layered Elastic Model
A layered elastic model can compute stresses, strains and deflections at any point in a pavement structure resulting from the application of a surface load. Layered elastic models assume that each pavement structural layer is homogeneous, isotropic, and linearly elastic. In other words, it is the same everywhere and will rebound to its original form once the load is removed. Layered elastic models for rigid pavement use the same principles as those for flexible pavements. To read the layered elastic discussion, see Layered Elastic Model.
Finite Elements Model
The finite element method (FEM) is a numerical analysis technique for obtaining approximate solutions to a wide variety of engineering problems. Although originally developed to study stresses in complex airframe structures, it has since been extended and applied to the broad field of continuum mechanics (Huebner et al., 2001[1]). In a continuum problem (e.g., one that involves a continuous surface or volume) the variables of interest generally possess infinitely many values because they are functions of each generic point in the continuum. For example, the stress in a particular element of pavement cannot be solved with one simple equation because the functions that describe its stresses are particular to its specific location. However, the finite element method can be used to divide a continuum (e.g., the pavement volume) into a number of small discrete volumes in order to obtain an approximate numerical solution for each individual volume rather than an exact closed-form solution for the whole pavement volume. Fifty years ago the computations involved in doing this were incredibly tedious, but today computers can perform them quite readily.
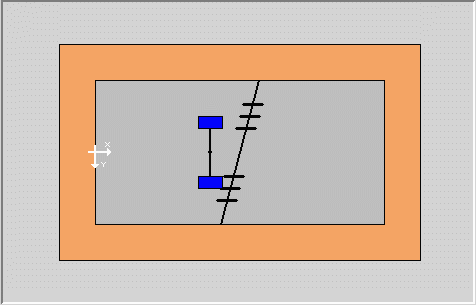
Much of the discussion in this section is identical to that of Finite Elements Model (the flexible pavement FEM). However, this section uses EverFE, a FEM developed at the University of Washington for the Washington State DOT and U.S. Army Corps of Engineers by Davids, Turkiyyah and Mahoney (1998[2]). As in flexible pavements, the FEM analysis of a rigid pavement discritizes the region of interest (the pavement and subgrade) into a number of elements with the loads at the top (see Figure 1).

Assumptions
The FEM approach works with a more complex mathematical model than the layered elastic approach so it makes fewer assumptions. Generally, FEM must assume some constraining values at the boundaries of the region of interest. Additionally, the choice of element geometry (size and shape) as well as interpolation functions will influence overall model performance.
Inputs
The typical finite elements method approach involves the following seven steps (Huebner et al., 2001[1]):
- Discretize the Continuum. The region of interest is divided into small discrete shapes.
- Select Interpolation Functions. Nodes are assigned to each element and then a function is chosen to interpolate the variation of the variable over the discrete element.
- Find the Element Properties. Using the established finite element model (the elements and their interpolation functions) to determine matrix equations that express the properties of the individual elements.
- Assemble the Element Properties to Obtain the System Equations. Combine the matrix equations expressing the behavior of the elements and form the matrix equations expressing the behavior of the entire system.
- Impose the Boundary Conditions. Impose values for certain variables at key boundary positions (e.g., the bottom and sides of the chosen region of analysis).
- Solve the System Equations. The above process results in a set of simultaneous equations that can then be solved.
- Make Additional Computations If Desired. The unknowns are displacement components. From these displacements element strains and stresses can be calculated.
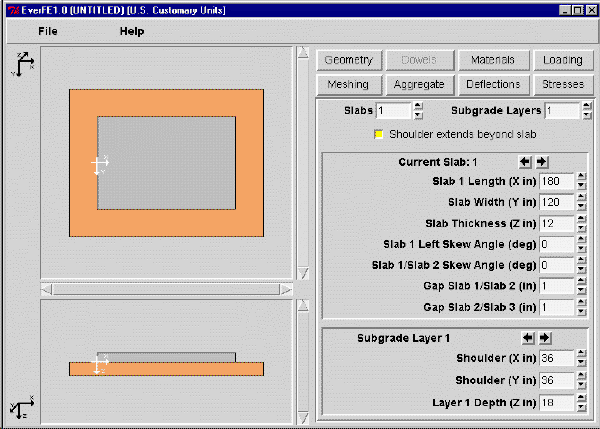
Figure 2 shows a screenshot of one EverFE input screen.
Outputs
The outputs of a FEM analysis are the same as for a layered elastic model:
- Stress. The intensity of internally distributed forces experienced within the pavement structure at various points. Stress has units of force per unit area (N/m2, Pa or psi).
- Strain. The unit displacement due to stress, usually expressed as a ratio of the change in dimension to the original dimension (mm/mm or in/in). Since the strains in pavements are very small, they are normally expressed in terms of microstrain (10-6).
- Deflection. The linear change in a dimension. Deflection is expressed in units of length (mm or µm or inches or mils).
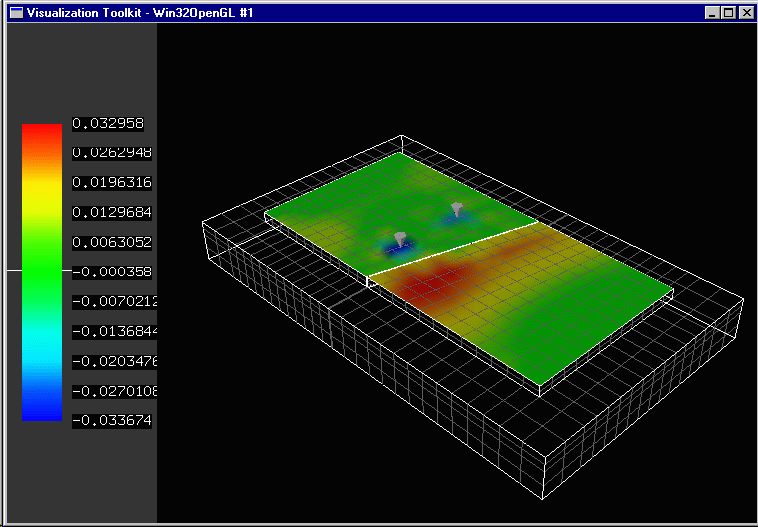
In addition, the finite elements method allows for extremely powerful graphical displays of these values.
Screen Shot Thumbnails from EverFE (Davids, Turkiyyah and Mahoney, 1998[2]). EverFE is a project developed at the University of Washington and expanded upon at the University of Maine. The project is supported by the Washington State Department of Transportation. Additional support is provided by the US Army Corps of Engineers