The following is a simple example of a set of control charts that could be used for HMA in-place air voids. Actual paving data from the Washington State Department of Transportation (WSDOT) is used for all charts. Typically, since contractors are most concerned with specification limits, control charts are set up to compare production material to specification limits. However, often in the case of in-place air voids, only a lower limit is specified. Therefore, it makes sense to start with this limit on the control chart and plot in-place air voids (See Figure 1). Note that there are no specified limits for the sample range, so no limits are shown on the R chart.
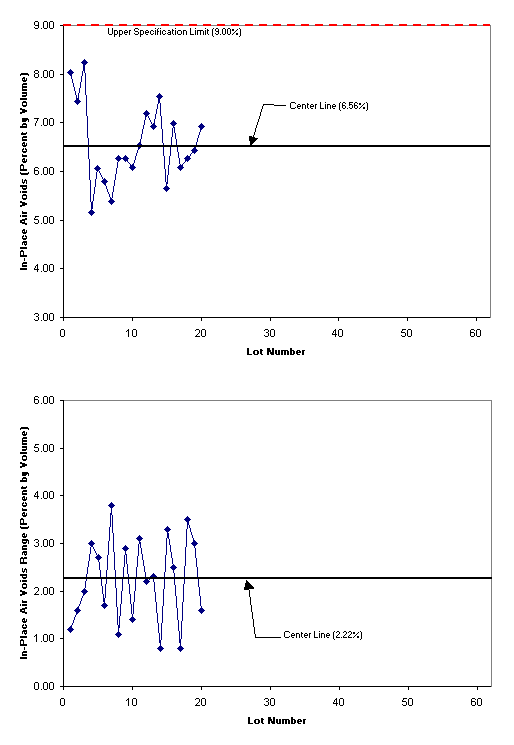
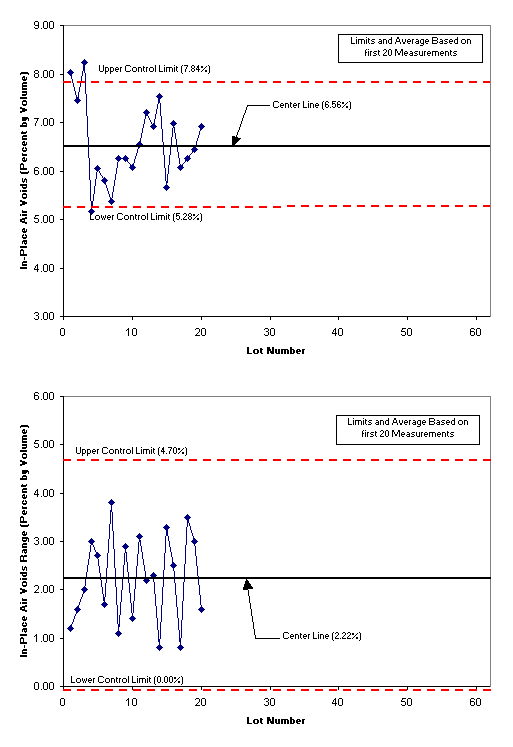
Using the control chart shown in Figure 1, it looks as if the process is well below the specification and all is well. After a certain number of samples, usually about 20 to 25 (Montgomery, 1997[1]), upper and lower control limits can be established to further monitor the process. Keep in mind, these limits are not specification limits and are only based on the averages and ranges of actual measurements. Most statistical quality control texts or programs contain charts or can automatically calculate where the upper and lower control limits should be based on average values, average sample ranges and sample size. In this case, each data point represents the average of five samples (in the x chart) and the range of these five samples (in the R chart).
The limits established in Figure 2 can be used to monitor the rest of the process. Measurements outside the limits represent an out-of-control process and should trigger investigation into possible causes. Notice that three of the first four in-place air void samples are outside the control limits. This is okay because these occurred on the test strip – the portion of the job where more variation is allowed as the contractor attempts to establish process control.
After 40 measurements (40 lots), the control charts now look like Figure 3. Note that in the x chart the process seems to have shifted down to some new lower average. In general, this is a good shift because lower air voids are generally better. However, this shift to lower air voids should also trigger a check of asphalt content to ensure that it is not caused by a high out of specification asphalt content. Note also that the range control chart shows the sample ranges have increased slightly. Assuming lower air voids are desirable, it would be prudent to adjust the control limits at this point to reflect the changed process. Figure 3 shows the new control limits, which are based on measurements 20 through 40 (lots 20 through 40).
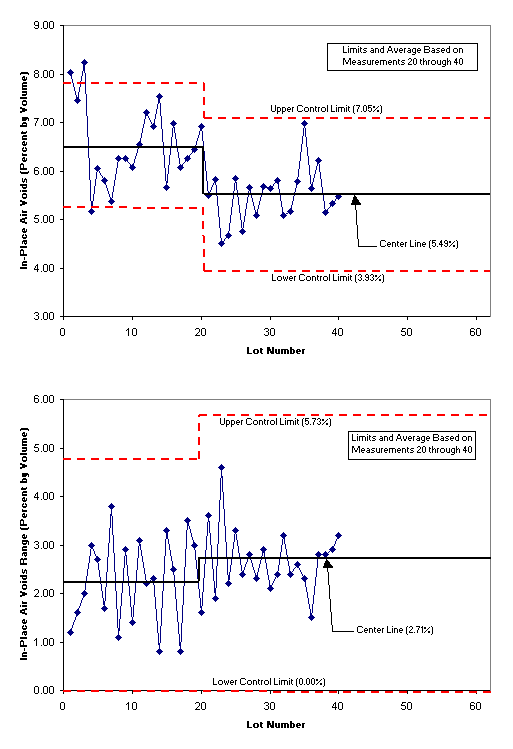
Figure 4 shows the entire process. Note that the average in-place air voids have increased from measurement 40 (lot 40) to the end, which should trigger an investigation to determine the cause. Measurement range seems to have stayed relatively consistent from measurement 20 (lot 20) to the end.
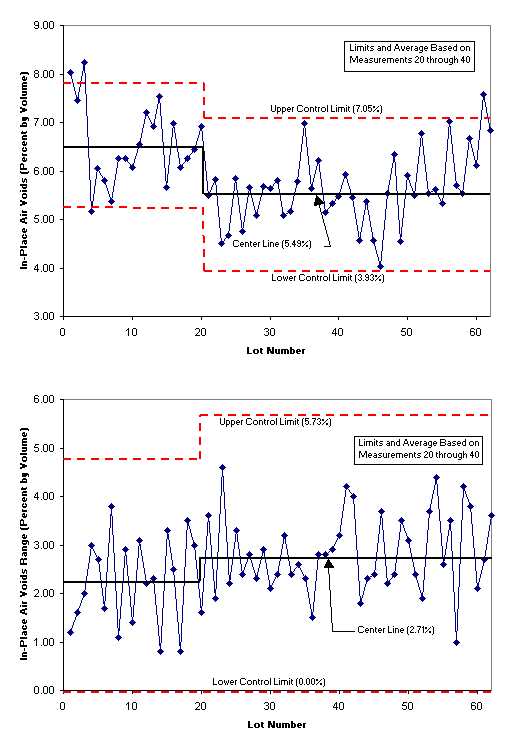
As demonstrated by this example, control charts can assist in quality control. Although in-place air voids were within specification for the entire project, the control chart allowed us to locate two process shifts (at approximately lot 20 and lot 50) that may have otherwise gone undetected. If we could have determined what caused in-place air voids to decrease at lot 20 then we may have been able to prevent their increase at lot 50. Additionally, any knowledge gained could be used on future jobs to further reduce in-place air voids and their variability.
- Introduction to Statistical Quality Control, 3rd Ed. John Wiley & Sons, Inc. New York, NY.↵
