How a pavement responds to applied stresses determines how it will behave structurally. Stresses and the resultant pavement response are the combined result of loading, environment, subgrade and pavement material characteristics. This section presents the typical stresses and stress characteristics experienced by a flexible pavement structure under load.
There are a variety of ways to calculate or at least account for these stresses in design. The empirical approach uses the AASHO Road Test results to correlate measurable parameters (such as subgrade resilient modulus) and derived indices (such as the structural number and pavement serviceability index) to pavement performance. The mechanistic-empirical approach relates calculated pavement stresses to empirically derived failure conditions.
Stress
The stresses that occur in a flexible pavement under load are quite complex. Although rigid pavement stresses have been routinely calculated since the 1920s, routine calculation of flexible pavement stresses is a more recent development. First, two-dimensional layered elastic programs offered desktop computers the ability to calculate these stresses. More recently, three-dimensional finite element programs have allowed more exact and detailed calculations.
Two-Dimensional Layered Elastic Model
Using a two-dimensional layered elastic model, the basic relationships between layer stiffness and stress for a two-layer flexible pavement structure is shown in Figure 1. In reality, stress distributions are more complex, however the basic relationships hold true. This additional complexity is further elaborated on in Three-Dimensional Finite Elements Modeling below.
Three-Dimensional Finite Elements Model
Because of the complex nature, a finite elements model is needed to get a good approximation of how a flexible pavement responds to loading. The complex stress and strains for a two-layer flexible pavement structure are shown graphically in Figure 2 using a three-dimensional finite elements model.
Deflection
HMA pavements are often described as “flexible” because they deflect under load. Figure 3 shows schematically how pavements deflect under load. FWDs can be used to accurately determine deflection characteristics of in-service pavements.
Multi-Layer System
The majority of pavement structures are more complicated than the two-layer system discussed above. Usually a base layer with or without an underlying subbase layer are placed between the asphalt concrete and subgrade. These layers may be either unbound or stabilized granular materials which have distinctly different properties from the surface and subgrade layers. One can imagine that the solutions for systems with three or more layers become increasingly more complex.
For a three-layer pavement, several charts and tables have been developed by Peattie, Jones and Fox (Yoder and Witczak, 1975[1]) to determine the stresses, strains, and deflections. Peattie (1962[2]) developed graphical solutions for vertical stress in three-layer systems. Jones (1962[3]) presented solutions for horizontal stresses in a tabular form. Both of these solutions were based upon a Poisson’s ratio of 0.5 for all layers.
The logical extension of these solutions was the development of computer programs in order to expedite analysis and allow greater flexibility in accommodating material properties and multiple loads. Even the most elementary of these allow for materials with Poisson’s ratios other than 0.5. Some are capable of ascertaining the effects of multiple wheel configurations and/or nonlinear material behavior. During the 1980s, as these mainframe computer programs were converted to run on microcomputers, a greater potential was developed to use elastic analysis tools in pavement design and rehabilitation decision making.
Typical input required for using these computer programs include:
- Material properties of each layer
- Modulus of elasticity
- Poisson’s ratio
- Thickness of each pavement layer
- Loading conditions (2 of 3 listed below)
- Magnitude of load
- Radius of load
- Contact pressure
- Number of loads
- Location of load(s) on the surface (x,y coordinates)
- Location of analysis points for output (x,y,z coordinates)
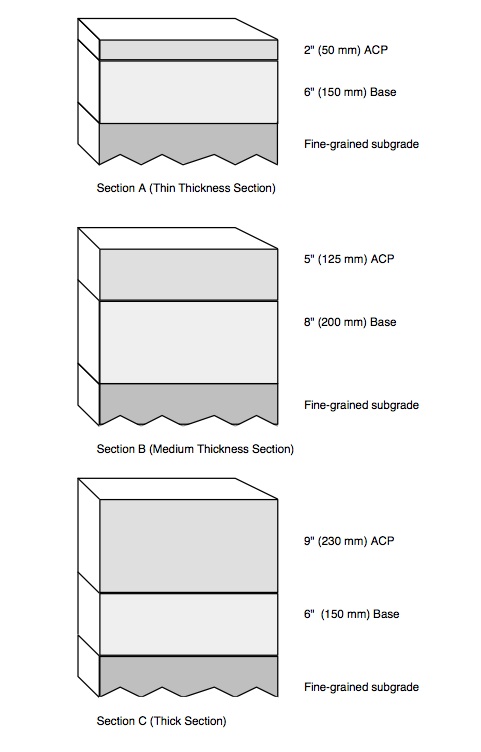
For the purposes of illustration, three typical pavement cross-sections have been selected as shown in Figure 4. The initial conditions we will examine are:
- Material properties of each layer
| Layer | Elastic Modulus | Poisson’s Ratio | |
| psi | MPa | ||
| Asphalt Concrete | 500,000 | 3450 | 0.35 |
| Crushed Stone Base | 25,000 | 172 | 0.40 |
| Fine-grained Subgrade | 7,500 | 52 | 0.45 |
- Layer Thicknesses
| Section | AC Thickness | Base Thickness | ||
| in | mm | in | mm | |
| A | 2 | 50 | 6 | 150 |
| B | 5 | 125 | 8 | 200 |
| C | 9 | 230 | 6 | 150 |
- Loading Conditions
- Magnitude of Tire Load = 9,000 lbs (40 kN)
- Tire Pressure = 80 psi (552 kPa)
- Number of Loads = 1
- Location of Load:
- x = 0
- y = 0
- Location of Analysis Points (all at x=0, y=0)
- Surface Deflection (all at z=0)
- Horizontal Tensile Strain at Bottom of ACP
| Thin Pavement: z = 2 in (50 mm) |
| Medium Pavement: z = 5 in (125 mm) |
| Thick Pavement: z = 9 in (230 mm) |
- Vertical Compressive Strain at Top of Subgrade
| Thin Pavement: z = 8 in (200 mm) |
| Medium Pavement: z = 13 in (330 mm) |
| Thick Pavement: z = 15 in (380 mm) |
A layered elastic analysis was performed using the inputs as defined above, and the results are listed in Table 1 under the heading “Standard Pavement”. As would be expected, the surface deflection, the horizontal strain at the bottom of the AC, and the vertical compressive strain at the top of the subgrade all decrease with increasing pavement thickness. A comparison of FWD basins for the three standard sections is given in Figure 5.
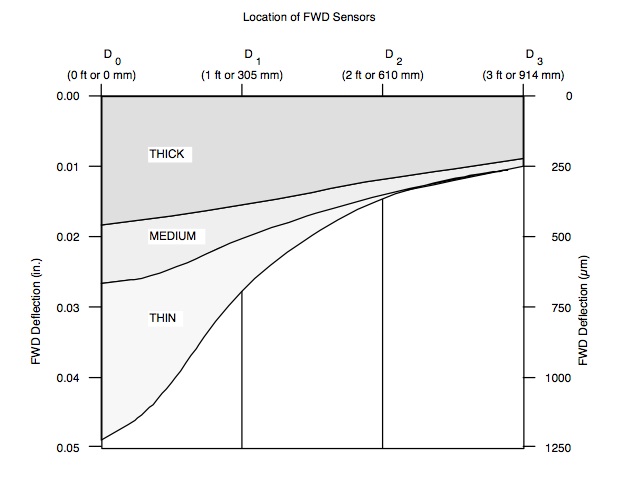
Table 1: Sensitivity Analysis of Various Input Parameters
| Pavement Response Parameter | Standard Pavement | Low Tire Load | High Tire Pressure | Stabilized Subgrade | Asphalt Treated Base | Moisture Sensitive | ||||||
| inches | mm | inches | mm | inches | mm | inches | mm | inches | mm | inches | mm | |
| 1. Surface deflection top of AC | ||||||||||||
| 1.1 Section A (thin) | 0.048 | 1.219 | 0.006 | 0.152 | 0.052 | 1.321 | 0.036 | 0.914 | 0.021 | 0.533 | 0.053 | 1.346 |
| 1.2 Section B (med) | 0.027 | 0.686 | 0.003 | 0.076 | 0.028 | 0.711 | 0.023 | 0.584 | 0.014 | 0.356 | 0.033 | 0.838 |
| 1.3 Section C (thick) | 0.018 | 0.457 | 0.002 | 0.051 | 0.019 | 0.483 | 0.016 | 0.406 | 0.012 | 0.305 | 0.024 | 0.610 |
| 2. Horizontal tensile strain bottom of AC or ATB (x 10-6) | ||||||||||||
| 2.1 Section A (thin) | 469 | 121 | 735 | 369 | 193 | 482 | ||||||
| 2.2 Section B (med) | 279 | 44 | 352 | 246 | 88 | 433 | ||||||
| 2.3 Section C (thick) | 145 | 17 | 17 | 128 | 161 | 258 | 128 | 67 | 258 | |||
| 3. Vertical compressive strain top of subgrade (x 10-6) | ||||||||||||
| 3.1 Section A (thin) | -2,239 | -284 | -2,554 | -956 | -508 | -2,604 | ||||||
| 3.2 Section B (med) | -755 | -79 | -790 | -431 | -222 | -1,037 | ||||||
| 3.3 Section C (thick) | -371 | -371 | -38 | -375 | -375 | -245 | -245 | -169 | -169 | -608 | -608 | |
Note: Tension (+), Compression (-)
In order to demonstrate the sensitivity of the analysis to load and material changes, several other cases were run and compared to the Standard Pavement. These included:
- Low Tire Load: Tire load decreased from 9,000 lb (40 kN) at 80 psi (552 kPa) to 900 lb (4 kN) at 30 psi (207 kPa). This is a comparison of the effects of a truck load versus a passenger vehicle.
- High Tire Pressure: Increase from 80 psi (552 kPa) to 140 psi (965 kPa). This demonstrates the difference in pavement response from a standard truck tire pressure to one which is an extreme.
- Stabilized Subgrade: Increase subgrade modulus from 7,500 psi (52 MPa) to 50,000 psi (345 MPa) in the top 6 in (150 mm) of soil. This case shows the effect of subgrade improvement.
- Asphalt Treated Base: Increase base course modulus from 25,000 psi (172 MPa) to 500,000 psi (3450 MPa). This represents an increase in the structural capacity of the pavement.
- Moisture Sensitive: Decrease AC modulus from 500,000 psi (3450 MPa) to 200,000 psi (1380 MPa). This illustrates a weakening of the AC layer due to stripping in the mixture.
Comparisons between the “Standard Pavement” case and the modified input just described are given in Table 2.
| Section | Percent Change from Standard Pavement | |||
| Surface Deflection | Tensile Strain in AC | Compr. Strain in Subgrade | ||
| Low Tire Load | A | -88 | -74 | -87 |
| B | -89 | -84 | -90 | |
| C | -89 | -88 | -90 | |
| High Tire Pressure | A | +8 | +57 | +14 |
| B | +4 | +26 | +5 | |
| C | +6 | +11 | +1 | |
| Stabilized Subgrade | A | -25 | -21 | -57 |
| B | -15 | -12 | -43 | |
| C | -11 | -12 | -34 | |
| Asphalt Treated Base | A | -56 | -59 | -77 |
| B | -48 | -68 | -71 | |
| C | -33 | -54 | -54 | |
| Moisture Sensitive | A | +10 | +3 | +16 |
| B | +22 | +55 | +37 | |
| C | +33 | +78 | +64 | |
As would be expected, there is a dramatic decrease (on the order of 75 to 90 percent) in all of the pavement response parameters when a passenger vehicle loading is compared to that of a truck load. These decreases become even more meaningful when they are discussed in the context of pavement life later on in these notes.
The increase in tire contact pressure from 80 to 140 psi (552 to 965 KPa) results primarily in an increase in the tensile strain in the asphalt concrete. This parameter increased 11 percent for the thick pavement and 57 percent in the thin pavement. It is interesting to note
that very little change in the surface deflection or compressive strain in the subgrade resulted from the higher tire pressure. In general, the surface layer of the pavement is sensitive to changes in tire pressure, particularly “thin” surface courses. The lower layers are most sensitive to changes in load.
The incorporation of a stabilized subgrade layer affected the vertical compressive strain in that layer most effectively, although significant improvement in the surface deflection and tensile strain in the asphalt surface can be noted for the thin pavement. The use of an asphalt treated base greatly influenced the response parameters in all three pavement sections.
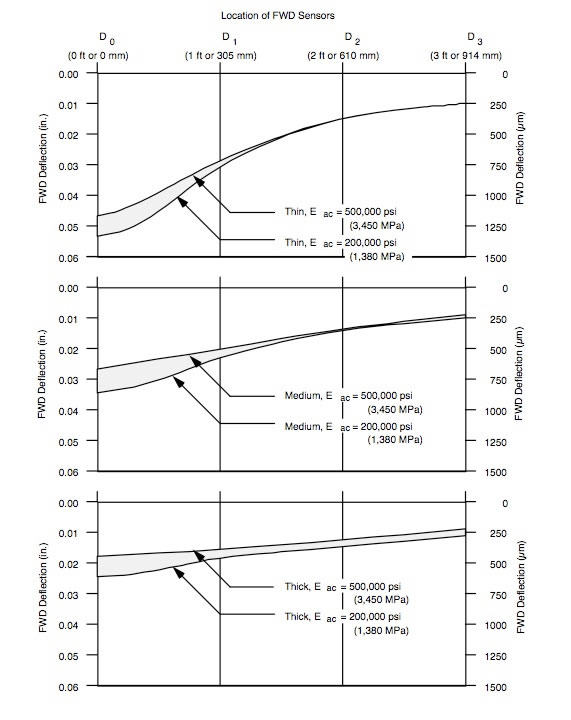
The thick pavement, Section C, demonstrated the greatest increase in pavement responses to the presence of a moisture susceptible asphalt mixture. Section A was the least affected of the three. Further illustration of the effects of a weaker surface layer is presented for all
three sections in the FWD basins shown Figure 6.
- Yoder, E.J. and Witczak, M.W., Principles of Pavement Design, 2nd Ed., John Wiley & Sons, New York, 1975.↵
- Peattie, K.R., “Stress and Strain Factors for Three-Layer Elastic Systems,” Highway Research Board Bulletin 342, Highway Research Board, 1962.↵
- Jones, A., “Tables of Stresses in Three-Layer Elastic Systems,” Highway Research Board Bulletin 342, Highway Research Board, 1962.↵
