At first glance, this equation looks quite complex – it is.

| Where: | W | equals | axle applications inverse of equivalency factors (where W18 = number of 18,000 lb (80 kN) single axle loads) |
| Lx | equals | axle load being evaluated (kips) | |
| L18 | equals | 18 (standard axle load in kips) | |
| L2 | equals | code for axle configuration 1 = single axle 2 = tandem axle 3 = triple axle (added in the 1986 AASHTO Guide) x = axle load equivalency factor being evaluated s = code for standard axle = 1 (single axle) |
|
| G | equals | ||
| Pt | equals | 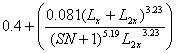 "terminal" serviceability index (point at which the pavement is considered to be at the end of its useful life) "terminal" serviceability index (point at which the pavement is considered to be at the end of its useful life) |
|
| b | equals | function which determines the relationship between serviceability and axle load applications | |
| SN | equals | structural number |
Example Calculation for a Single Axle
- Assumptions: Single axle, 30,000 lb (133 kN), SN = 3, pt = 2.5
- Answer: (Table D.4, p. D-6, 1993 AASHTO Guide) = 7.9
- Calculations
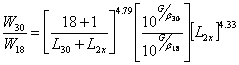
| where : | W18 | equals | predicted number of 18,000 lb (80 kN) single axle load applications |
| W30 | equals | predicted number of 30,000 lb (133 kN) single axle load applications | |
| Lx | equals | L30 = 30 | |
| L2x | equals | 1 (single axle) | |
| G | equals | serviceability loss factor | |
| equals | |||
| b30 | equals | curve slope factor | |
| equals | 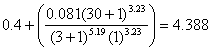 |
||
| and | G/b30 | equals | -0.2009/4.388 = -0.04578 |
| b18 | equals | 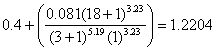 |
|
| G/b18 | equals | -0.2009/1.2204 = -0.1646 | |
| Thus | 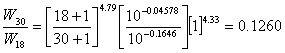 |
||
| and | |||
| Finally | LEF | equals | |
Example Calculation for a Tandem Axle
- Assumptions: Tandem axle, 40,000 lb (133 kN), SN = 5, pt = 2.5
- Answer: (Table D.5, p. D-7, 1993 AASHTO Guide) = 2.08
- Calculations
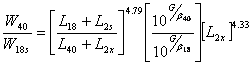
| where : | L40 | equals | 40 (tandem axle) |
| L18 | equals | 18 (single axle) | |
| L2x | equals | 2 (tandem axle) | |
| L2s | equals | 1 (single axle) | |
| G | equals | serviceability loss factor | |
| equals | |||
| b40 | equals | curve slope factor | |
| equals | 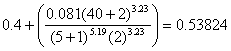 |
||
| and | G/b40 | equals | -0.2009/0.53824 = -0.37325 |
| b18 | equals | 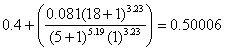 |
|
| G/b18 | equals | -0.2009/0.50006 = -0.40175 | |
| Thus | |||
| Finally | LEF | equals | |
