In general, control charts are used to plot production values and variation over time. These charts can then be analyzed to determine if changes in production values or variation are due to the inherent variability of the process or a specific correctable cause. Control charts for variables are fairly straightforward and can be quite useful in material production and construction situations. Four popular control charts within the manufacturing industry are (Montgomery, 1997[1]):
- Control chart for variables. In variable sampling, measurements are monitored as continuous variables. Because they retain and use actual measurement data, variable sampling plans retain more information per sample than do attribute sampling plans (Freeman and Grogan, 1998[2]). This implies that compared to attribute sampling, it takes fewer samples to get the same information. Because of this, most statistical acceptance plans use variable sampling.
- Control chart for attributes. This chart is used when a number cannot easily represent the quality characteristic. Therefore, each item is classified as “conforming” or “nonconforming” to the particular specification for the quality characteristic being examined. These charts look similar to control charts for variables but are based on a binomial distribution instead of a normal distribution. Two of the most common attribute control charts are for fraction nonconforming and defects.
- Cumulative sum control chart. A disadvantage of control charts for variables and attributes is that they only use data from the most recent measurement to draw conclusions about the process. This makes it quite insensitive to shifts on the order of 1.5 standard deviations or less. The cumulative sum control chart is a more sensitive control chart that can use information from an entire set of points to draw conclusions about the process. Basically the cumulative sum (or cusum) chart plots the cumulative sum of measurement deviations from an average. Therefore, if an abnormal amount of measurements fall on only one side of the average this sum will grow and indicate an out-of-control condition.
- Exponentially weighted moving average (EWMA) control chart. This chart is similar to the cumulative sum chart but instead of weighting each measurement the same, recent measurements are more influential because measurements are weighted exponentially based on when they were made.
Beyond these, control charts begin to get more complex or are hybrids of more than one type.
Control Charts for Variables
Control charts for variables are fairly straightforward and can be quite useful in HMA production and construction situations. The following paragraphs describe the basic concepts involved in a control chart for variables.
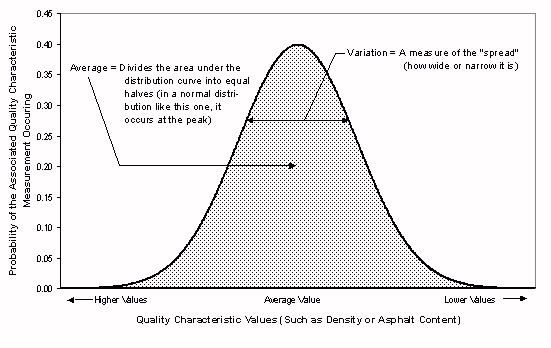
First, variation needs to be quantified. Variation can be represented in many different ways, one of which is the probability distribution (see Figure 1).
Mathematically, variation is described as “variance”:
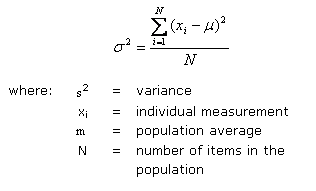
This equation is true when the entire population is known (e.g. every item produced has been measured or tested). This is a rarity; typically the population is only sampled and therefore only the measurements of a select few items (or locations) are known. In this case, the equation becomes:
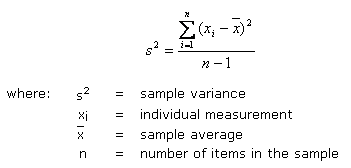
Variance is described by a squared quantity. This is necessary to prevent positive and negative differences between individual measurements and the average from canceling each other out. Unfortunately, this results in variation units also being squared. Therefore, if the material characteristic is density (kg/m3 or lb/ft3) then the variation is (kg/m3)2 or (lb/ft3)2, which is not a meaningful quantity. Therefore, the square root of variation, the standard deviation, is typically discussed:
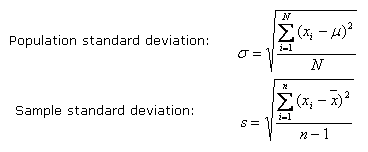
Second, all processes contain a certain amount of random variation. This inherent variation may come from machine precision limits, small variations in raw material characteristics, small variations in workers’ ability and so forth. The keys to controlling variation are knowing when variation is due to inherent random variability and when variation is caused by a non-random aspect associated with the process. If the variation is associated with the process, it can presumably be reduced. Distinguishing between these two types of variation involves observing a process that is “in control” (variation is only due to the inherent variability), then setting upper and/or lower control limits that contain this variation. Then, any measurements outside these limits are due to something induced by the production process. Typically these upper and lower control limits are set at 3s (3 standard deviations) on either side of the target value. Assuming the measured material characteristic is normally distributed, a statistical hypothesis test will show that there is only a 0.27 percent chance that a measurement will be outside of the control limits and thus generate a “false alarm”. Therefore, one can be fairly certain that measurements outside the control limits are due to controllable factors.
Third, although sample standard deviation (s) is an acceptable way of estimating actual population standard deviation (s), the sample range (R, difference between the highest and lowest sample measurements) is adequate for the small sample sizes usually encountered in roadway construction. Since the sample range (R) is easiest to calculate, it is often used.
Finally, Figures 2 and 3 are typical control charts for x
(sample average) and R (sample range). This type of control chart is called a Shewhart control chart after Dr. Walter S. Shewhart who first proposed the general theory of control charts in 1924. This control chart can be used to monitor material quality characteristics such as HMA asphalt content, gradation or compaction, or PCC strength.
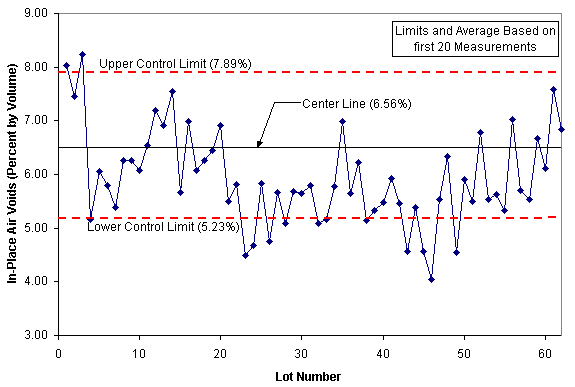
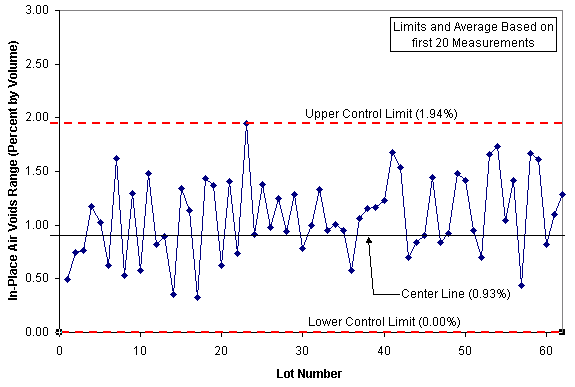
Often, samples are only taken one at a time (as in asphalt content monitoring) and therefore require a slightly different control chart – one that tracks individual measurements and a moving range (MR). Figures 4 and 5 show a control chart for individual measurements.
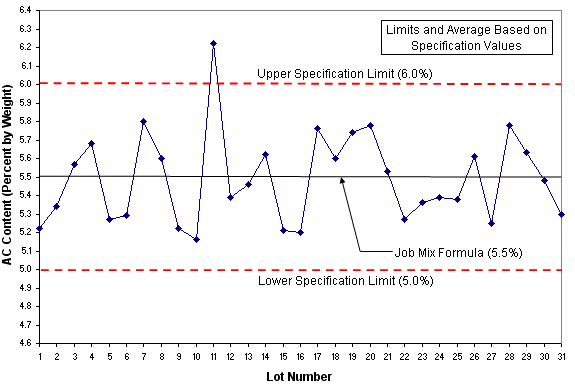
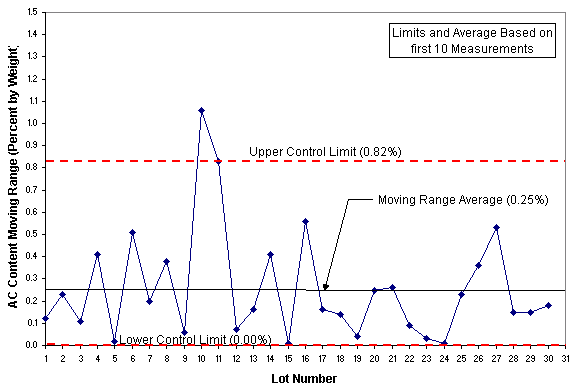
In general, as a process becomes more controlled, the upper and/or lower control limits can be decreased to reflect this. The general rule-of-thumb is to act when measurements exceed control limits. However, many companies have expanded on this and developed their own rules such as (Montgomery, 1997[1]):
- One or more points outside of the control limits.
- Two of three consecutive points outside the 2-s warning limits but still inside the control limits.
- Four of five consecutive points beyond the 1-s limits.
- A run of eight consecutive points on one side of the centerline.
- Six points in a row steadily increasing or decreasing.
- Fourteen points in a row alternating up and down.
- An unusual or non-random pattern in the data.
- One or more points near a warning or control limit.
