Acceptance sampling has been in general use for well over 60 years (Montgomery, 1997[1]). Therefore, the theoretical underpinnings behind acceptance sampling are well proven. The key is then to appropriately apply acceptance sampling and its associated statistics to the pavement construction industry to create a viable overall plan. Correct application involves proper implementation of the following acceptance sampling components:
- Acceptance sampling type
- Quality characteristics
- Specification limits
- Statistical model
- Quality level goals
- Risk
- Pay factors
Decisions regarding these components will significantly impact final acceptance plan performance.
Types of Acceptance Sampling
There are two basic types of acceptance sampling: (1) attribute sampling, and (2) variable sampling. Both attribute and variable sampling are used in pavement construction; however variable sampling is more prevalent (Bowery and Hudson, 1976[2]; Schmitt, et al., 1998[3]).
Attribute Sampling
In attribute sampling, each sample is inspected for the presence or absence of one or several attributes (often called quality characteristics). Measurements used to detect these quality characteristics are not retained. Rather, they are compared to a standard then recorded as either passing or failing. An aggregate fracture test is an example of attribute sampling. Aggregate is accepted or rejected based on a minimum quality characteristic of one fractured face on a specified percentage of the material. The actual percentage of fractured face is not recorded; instead, a simple pass-fail record is used.
Variable Sampling
In variable sampling, measured quality characteristics are used as continuous variables, which means that, unlike attribute sampling, measurement values are retained. Because these values are retained rather than converted into a discrete pass-fail criterion, variable sampling plans retain more information per sample than do attribute sampling plans (Freeman and Grogan, 1998[4]). This means that compared to attribute sampling, it takes fewer variable samples to get the same information. Because of this, most statistical acceptance plans use variable sampling.
However, variable sampling does have disadvantages. Foremost, variable sampling plans are predicated on a known distribution of the measured property. Therefore, most variable sample plans assume a normal distribution of the measured property. For instance, acceptance testing for HMA compaction often assumes that in-place HMA densities (the measured property) are normally distributed. If this normal distribution assumption is not true then the resulting estimates of lot quality will be wrong. Fortunately, construction-related lot characteristics are usually normally distributed (Markey, Mahoney, and Gietz, 1994[5]; Aurilio and Raymond, 1995[6]; Cadicamo, 1999[7]).
Therefore, although both attribute and variable sampling are used in pavement construction, variable sampling is more prevalent because it provides more information per sample and its necessary assumption of a normal distribution of the quality characteristic is usually satisfied.
Quality Characteristic Selection
Quality characteristics are those material characteristics or properties that a particular acceptance plan measures to determine quality. Quality characteristics can be any measurable material or construction property but they must be carefully selected for two reasons: (1) their quality should accurately reflect overall project quality and (2) they should be relatively independent of one another.
Construction contracts, including pavement contracts, generally require full payment at substantial completion. However, since the constructed pavement performs for many years after construction, contracting agencies usually use some predictive method to relate construction quality to long-term pavement performance. Statistical acceptance plans typically accomplish this by choosing construction quality characteristics that are most predictive of pavement performance. These quality characteristics typically include mix properties (such as aggregate gradation, HMA asphalt content and PCC slump), HMA in-place density, PCC strength, and pavement smoothness (Schmitt, et al., 1998[3]).
Quality characteristics must also be chosen to avoid correlation with one another. If not carefully selected, a change in one quality characteristic (such as aggregate gradation) could result in a change in another quality characteristic (such as HMA VMA or PCC cement content). Lin, Solaimanian, and Kennedy (2001[8]) point out that this correlation will always cause biases in pay factor determination. In the gradation-VMA instance mentioned previously, the bias occurs because a poorly graded aggregate would be penalized not only by lower pay for poor gradation but also by lower pay for the correlated poor VMA. Bias in the opposite direction (higher pay for well-graded aggregate) is equally likely. Therefore, biased pay factors will unfairly penalize either the agency or the contractor.
Acceptance sampling determines overall construction quality by measuring quality characteristics. Proper selection of these characteristics ensures that (1) their quality accurately reflects construction quality, which should in turn reflect long-term pavement performance and (2) they are relatively independent of one another so that final pay is not biased in either direction.
Specification Limits
Specification limits for quality characteristic measurements are established to differentiate between adequate material and inadequate (or defective) material. For instance, a lower specification limit for PCC 28-day compressive strength might be 20.7 MPa (3,000 psi). Therefore, a measurement of 20.7 MPa (3,000 psi) or higher represents adequate strength while a measurement below 20.7 MPa (3,000 psi) represents inadequate strength.
Specification limits must be based on sound engineering judgment and sound statistical analysis. Specifically, engineering judgment is used to establish a target value for each quality characteristic and statistical analysis is used to establish an acceptable range around the target value. This range is used to account for the various sources of variability inherent in producing and testing HMA. Specifically, there are four types of variability to consider: (Hughes, 1996[9]):
- The material’s inherent variability is the true random variation of the material and is a function of material characteristics alone. A contractor’s manufacturing and construction process cannot control this variability.
- Sampling variability is the variation in sample characteristics from sample-to-sample that is attributable to variations in sampling technique. A contractor’s manufacturing and construction process cannot control this variability.
- Testing variability is the lack of repeatability of test results. Operators, equipment condition, calibration, and test procedure all contribute to testing variability. A contractor’s manufacturing and construction process cannot control this variability.
- Manufacturing and construction variability is the variation in material caused by the manufacturing and construction process. These variations can be extremely localized within a lot and therefore difficult to detect by random sampling (like density differentials and pavement thickness variations) or they can be more global (e.g., between lots or days) and therefore more easily detected by random sampling (like changes in water-cement ratio, asphalt content or aggregate gradation between lots). Contractor quality control can minimize these types of variability.
The total variability is then the sum of the material, sampling, testing and manufacturing/construction variability:
Since contractors can only control manufacturing and construction variability, if the sum of inherent material, sampling and testing variability is greater than the allowable specification band, a potentially large amount of material will be judged out-of-specification for no contractor-correctible reason. For instance, an asphalt content specification of the JMF ± 0.1 percent does not make statistical sense because the combination of inherent asphalt content variability, sampling variability, and testing variability will typically cause test results to vary by more than ±0.1 percent from the JMF (Hughes, 1996[9]). A more practical approach, which adequately accounts for material, sampling, and testing variability might specify the JMF asphalt content ±0.5 percent. In sum, specification limits should be tight enough to detect manufacturing and construction variability, but loose enough to allow a reasonable amount of testing, sampling, and inherent material variability.
Statistical Model
The statistical model used by an acceptance plan determines how the plan relates actual random sample test results to the distribution of the quality characteristic within the lot. This distribution is then used to determine lot quality.
Statistical models all rely on random samples, which provide two pieces of data: (1) the average of the sample measurements and (2) the variation in sample measurements. Both pieces of data are needed to estimate the distribution of the measured quality characteristic within a lot (see Figure 1).
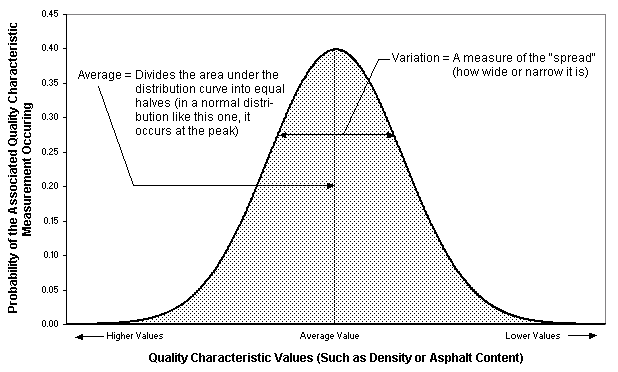
There are typically three different ways of using sample data:
- Use the average of sample measurements only. This method calculates the sample average and uses this to estimate lot average. It does not calculate sample variation, thus it is unable to estimate the overall distribution of the quality characteristic within the lot.
- Use the average of sample measurements and assume typical lot variation. This method estimates lot average as the calculated sample average and assumes a typical lot variation based on historical data of the measured quality characteristic. By assuming a typical lot variation, this method can use the standard normal distribution (a relatively well-understood distribution) to estimate the overall distribution of the quality characteristic within the lot. This estimate is only accurate if the actual variation of the quality characteristic within the lot is close to the assumed variation (Freeman and Grogan, 1998[4]).
- Use the average of sample measurements and variation in sample measurements. This method estimates lot average as the calculated sample average and estimates lot variation as the calculated sample variation. It estimates the overall distribution of the quality characteristic within the lot by applying the non-central t distribution (Johnson and Welch, 1940[10]).
Methods like #3 are typically preferable because they fully describe the distribution of the quality characteristic within a lot and make the fewest assumptions. However, methods such as #1 and #2 are still often used.
“Quality” is then defined as the fraction of the overall quality characteristic distribution that falls within specification limits. It is usually expressed as either (TRB, 1999[11]):
- Percent defective (PD) – also called percent nonconforming. The percentage of the lot falling outside specification limits.
- Percent within limits (PWL) – also called percent conforming. The percentage of the lot falling above a lower specification limit, below an upper specification limit, or between upper and lower specification limits. PWL is related to PD by the following: PWL = 100% – PD.
To summarize, the statistical model determines how and to what extent the overall quality characteristic distribution is estimated. Some models are quite simple and only estimate an average quality characteristic value while other models are more complete and estimate both average and variation, which then provides the ability to estimate lot quality. Lot quality, expressed as PWL, is simply the fraction of the lot that falls within specifications. Figure 2 presents a summary of the PWL concept and the common approaches to increase PWL.
Quality Level Goals (AQL and RQL)
Quality level goals consist of an acceptable quality limit (AQL) and a rejectable quality limit (RQL). AQL is the minimum level of actual quality at which the material or construction can be considered fully acceptable (TRB, 1999[11]). RQL is the maximum level of actual quality at which a material or construction can be considered unacceptable and thus, rejectable (TRB, 1999[11]).
The appropriate levels of AQL and RQL are matters of judgment. It would be nice but unrealistic to expect all material within a lot to meet specifications (PWL = 100). However, some small fraction of defective material must be permitted due to the unavoidable variability that accompanies any material or production process (Comisky, 1974[12] as cited in Freeman and Grogan, 1998[4]). To account for this, AQL should be some value less than 100 PWL. Additionally, AQL should also be set at a value equal to the maximum amount of defective material present within the pavement that will not substantially degrade overall road quality (Freeman and Grogan, 1998[4]). These considerations result in typical AQL values of 90 or 95 PWL.
RQL is generally set much lower than AQL because it should represent a PWL below which the pavement is essentially worthless to the contracting agency. Typical values of RQL range from 60 PWL down to 30 PWL and often depend upon sample size. If the actual material quality level is between AQL and RQL then it is often accepted at reduced pay because although defects in the material will degrade overall road performance they will not degrade it to a point where the pavement has no value.
AQL and RQL are difficult to accurately set. Typically there is not enough data to accurately relate material quality to final pavement worth. Although current research is addressing this issue (Weed, 1998[13]; Deacon et al, 2001[14]), most AQL and RQL values seem to be set using a combination of historical data, experience, and statistical tradition.
Risk
Using samples to make estimates about the quality of a large amount of construction material involves risk; there is some probability that a random sample will not be representative of the material as a whole, and will thus be an incorrect estimate of material quality. Therefore, risk is an inherent part of statistical acceptance plans. An incorrect estimate, or error, and its associated risk can be either of two types:
- Type I error (a risk). Acceptable construction quality will be rejected as unsatisfactory. This is the contractor’s (seller’s) risk and can result in unnecessary removal and reconstruction of large pavement sections. There are two types:
- Primary type I error (primary a risk). The contractor’s risk that material produced at AQL will be either rejected or subject to reduced pay.
- Secondary type I error (secondary a risk). The contractor’s risk that material produced at AQL will be rejected.
- Type II error (b risk). Unacceptable construction quality will be accepted as satisfactory. This is the contracting agency’s (buyer’s) risk and can result in additional maintenance costs, and premature pavement failure. There are two types:
- Primary type II error (primary b risk). The contracting agency’s risk that material produced at RQL will be accepted at bonus pay.
- Secondary type II error (secondary b risk). The contracting agency’s risk that material produced at RQL will be accepted.
These risks can be calculated and must be balanced. For a given sample size, reducing the likelihood of accepting poor material usually means increasing the likelihood of rejecting good material and vice versa (Freeman and Grogan, 1998[4]). To simultaneously reduce both of these risks, the sample plan must make more accurate estimates. This usually means increasing the sample size, which means higher inspection and testing costs to the contracting agency. Therefore, the contracting agency will try and achieve an acceptable balance between sample size (accuracy) and inspection and testing costs.
Selecting the appropriate contractor risk and contracting agency risk is a matter of judgment. However, these risks should be related to the criticality of the quality characteristic as well as economic considerations (Freeman and Grogan, 1998[4]). If the failure of a certain material characteristic will render an entire project useless, then it is a critical material characteristic. Therefore, the probability of accepting poor material (b risk) should be set quite small. Conversely, if a material characteristic is not critical, then the probability of accepting poor material (b risk) can be set higher (Freeman and Grogan, 1998[4]). For pavement construction, the primary a risk is often set near 5 percent and the primary b risk is often set near 10 percent (Cominsky, 1974[12] as cited in Freeman and Grogan, 1998[4]). As long as these risks are quantified and known in advance, both parties can account for them in their respective budgets and bids.
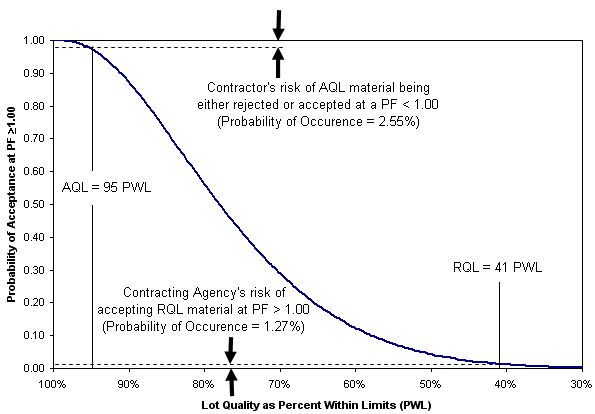
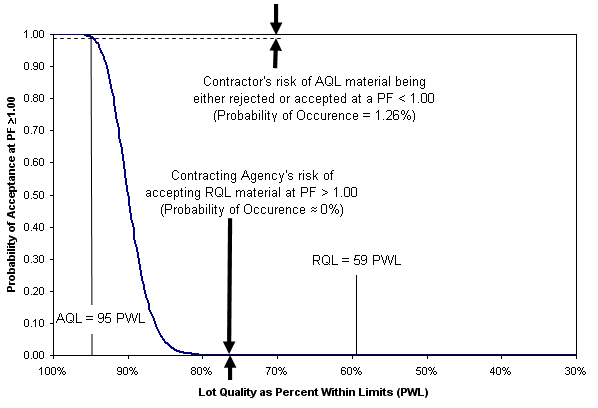
The risks involved in a particular acceptance plan are often expressed using an operating characteristic (OC) curve. An OC curve describes the relationship between a lot’s quality and its probability of acceptance for a given sample size. Each sample size has a different OC curve. Figure 3 shows a WSDOT OC curve for a sample size of five (n = 5). The better the sampling plan is at estimating actual lot quality, the steeper the OC Curve. Figure 4 shows a much steeper OC curve for a sample size of 50.
Pay Factors
Pay factors relate quality to actual pay. In broad terms, a pay factor (PF) is a multiple applied to the contract price of a particular item. Most acceptance plans apply a pay factor to the contract price based on the calculated quality (expressed as PD or PWL) of a particular quality characteristic. Pay factors usually range from a high between 1.00 and 1.12 down to a low between 0.50 and 0.75 (Mahoney and Backus, 2000[15]). Ideally, material produced at AQL receives a pay factor of 1.00, material produced at RQL is rejected, material produced between AQL and RQL receives a pay factor less than 1.00 depending on quality, and material produced in excess of AQL receives a pay factor greater than 1.00. Pay factors are not, however, as simple as they seem for two reasons: (1) expected pay is different than contractual pay and (2) material produced at AQL may not receive a 1.00 pay factor.
Expected Pay
First, the pay a contractor can expect for consistently producing material at a particular quality level is not necessarily the same as the pay factor shown in the specification for that quality level (referred to as the contractual pay factor).
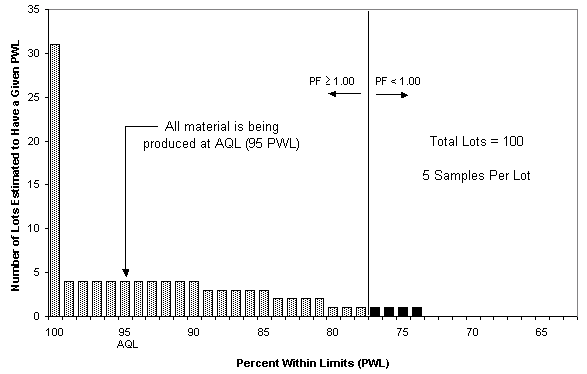
This difference occurs because sampling only estimates actual material quality. Therefore, material produced at AQL may be estimated by sampling to be either above or below AQL. Over time, sample estimates of quality will be normally distributed about a mean equal to the actual material quality. Figure 4 shows how this looks for material produced at AQL under a typical acceptance plan using an ideal normal distribution of samples (the large number of lots with estimated quality at 100 PWL occur because 100 PWL is the maximum achievable quality, therefore the entire portion of the normal distribution that falls above 100 PWL is represented by the 100 PWL value). Since each lot receives a contractual pay factor, Figure 6 shows the resulting pay factors associated with Figure 5. Figure 6 shows that material consistently produced at AQL (95 PWL) will not receive the contractual pay factor (1.04) associated with AQL but rather a lesser pay factor (1.0349 in this example). Simulations run by the FAA (FAA, 1999b[16]) and Weed (1995[17], 1998[13]) have also shown this type of behavior, which is a characteristic of almost all statistical acceptance plans that use pay factors.
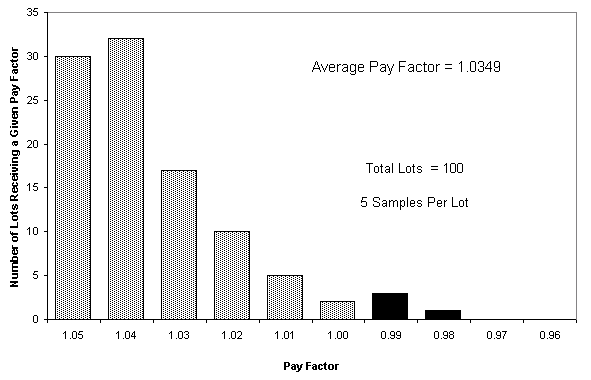
Pay Factor at AQL
Second, material produced at AQL does not always receive a 1.00 pay factor. In the example shown in Figures 6 and 7, AQL material produced a 1.0349 pay factor. Therefore, material produced at the contractually specified quality is paid at a higher rate than the contractually specified price. Conversely, in acceptance plans that do not include pay factors above 1.00, AQL material could receive a pay factor significantly less than 1.00. In these cases, material produced at the contractually specified quality is paid at a lower rate than the contractually specified price.
Pay factors relate material quality to actual pay. An ideal pay factor system typically allows bonus pay for material produced in excess of AQL, pays the contractual price for AQL material, applies a deduction for material produced between AQL and RQL and rejects material produced at or below RQL. Meeting all four of these goals is quite difficult because expected pay is often different than contractual pay and providing bonus pay for material produced in excess of AQL may lead to expected pay above the contractual price for AQL material.
- Introduction to Statistical Quality Control, 3rd Ed. John Wiley & Sons, Inc. New York, NY.↵
- National Cooperative Highway Research Program Synthesis of Highway Practice 38: Statistically Oriented End-Result Specifications. Transportation Research Board, National Research Council. Washington, D.C.↵
- Summary of Current Quality Control / Quality Assurance Practices for Hot-Mix Asphalt Construction. Transportation Research Record 1632. pp. 22-31.↵
- Statistical Acceptance Plan for Asphalt Pavement Construction. U.S. Army Corps of Engineers. Washington, D.C.↵
- Markey, Mahoney, and Gietz (1994). An initial evaluation of the WSDOT quality assurance specification for asphalt concrete.↵
- Development of End Result Specification for Pavement Compaction. Transportation Research Record 1491. pp. 11-17.↵
- A Partial Analysis of the Washington State Department of Transportation Quality Assurance Specification. Master’s Thesis. University of Washington. Seattle, WA.↵
- General Approach to Payment Adjustments for Flexible Pavements. Journal of Transportation Engineering (Jan/Feb 2001). pp. 39-46.↵
- National Cooperative Highway Research Program Synthesis of Highway Practice 232: Variability in Highway Pavement Construction. Transportation Research Board, National Research Council. Washington, D.C.↵
- Applications of the Non-Central t-Distribution. Biometrika, v.31, no. 3/4. pp. 362-389.↵
- Glossary of Highway Quality Assurance Terms. Transportation Research Circular, No. E-C010. Transportation Research Board, National Research Council. Washington, D.C.↵
- Session 18: Development of Acceptance Plans. Statistical Quality Control of Highway Construction. The Pennsylvania State University. University Park, PA. pp. 18.1-18.37.↵
- A Rational Method for Relating As-Built Quality to Pavement Performance and Value. Transportation Research Record 1632. pp. 32-39.↵
- Pay Factors for Asphalt-Concrete Construction: Effect of Construction Quality on Agency Costs DRAFT. Caltrans TM-UCB-PRC-2001-1. Sacramento, CA.↵
- QA Specification Practices. Washington State Transportation Center (TRAC). Seattle, WA.↵
- Engineering Brief No. 56: Development of Revised Acceptance Criteria for Item P-401 and Item P-501. FAA. Washington, D.C. ↵
- OCPLOT: PC Program to Generate Operation Characteristic Curves for Statistical Construction Specifications. Transportation Research Record 1491. pp. 18-26.↵
